是什么让OLTP数据库能够如此快速地查找数据？

Vu Trinh 2025-11-24 10:25:28

前言

作为一名数据工程师，我并没有花太多时间去使用像 PostgreSQL 这样的 OLTP 数据库。我知道，为了让数据库中的数据操作变快，必须有一些技术来提升数据库所支持典型工作负载的性能。对于 OLAP 系统来说，最终目标是尽可能多地剪枝数据。

对于 OLTP 系统来说，目标是尽可能快地找到一条记录。

但它们是怎么办到的呢？

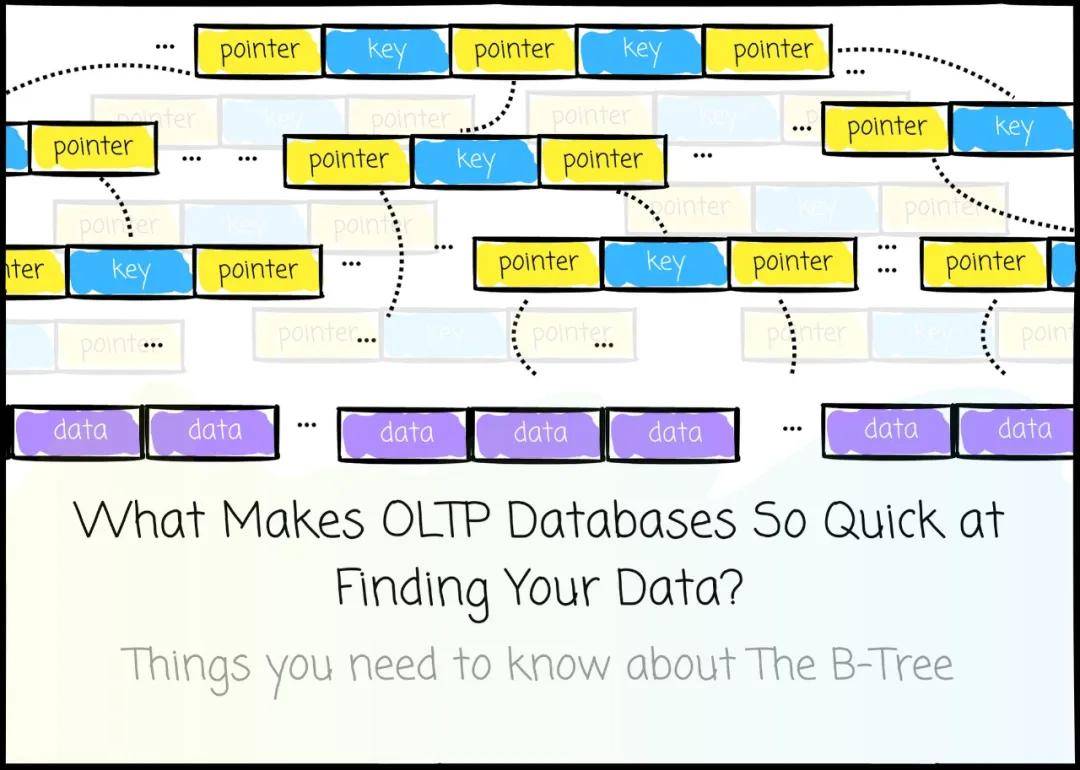
在本文中，我们将深入探讨在 PostgreSQL 和 MySQL 这类数据库中，用于优化查询性能的最流行技术：B-Tree。我们首先学习内存中树数据结构的基础知识，并利用这些知识逐步建立对 B-Tree 的理解。

一、树

在计算机科学中，树用来模拟一种层次结构。数据被安排在节点中，这些节点按层次链接。以下术语定义了任何树结构：

节点：一个单元，可能存储两样东西：数据和指向其他节点的指针（叶子节点没有指针）。
根：树的最顶端节点，它没有父节点。树从这里“开花”。
叶子节点：那些没有任何子节点的节点。
内部节点：它们连接根和叶子。它们至少有一个子节点。
父、子、兄弟：如果节点 A 指向两个节点 B 和 C，那么 A 是 B 和 C 的父节点，而 B 和 C 是 A 的子节点。拥有同一父节点的节点互为兄弟。

高度：树的高度是从根到任何叶子节点的最长路径。
子树：树中的任何节点都可以被视为子树的根。其下的所有节点，包括子节点、孙节点等，构成一棵更小的树。

深度：某个特定节点的深度是从根到该节点的路径长度。也就是说，根节点的深度为 0。

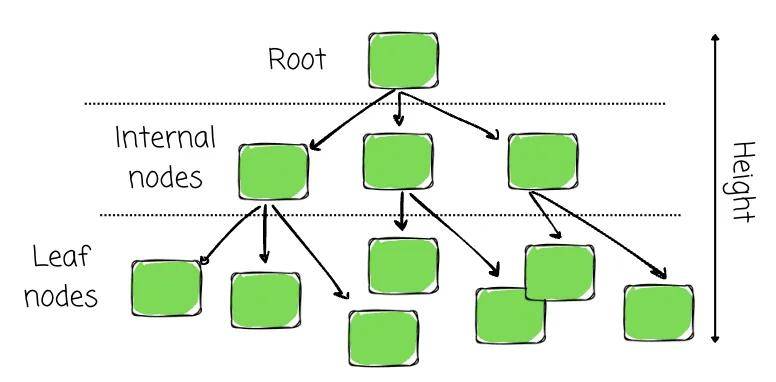
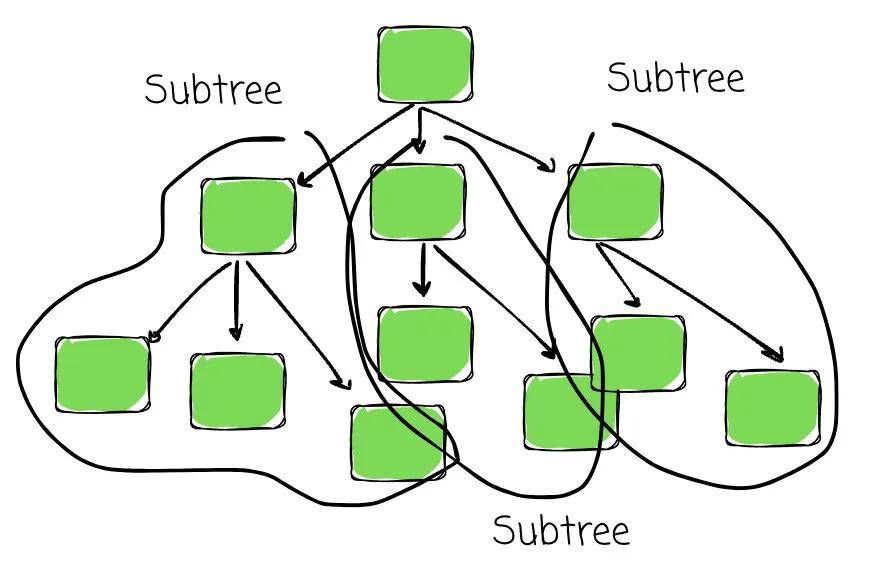
二、二叉树

数据结构的设计旨在以适合特定用例的方式促进数据的存储和检索。二叉搜索树（BST）是一种特殊形式，它提供了二分搜索性质。

对于不熟悉二分搜索的人来说，它是一种算法，将要搜索的值与有序数组的中间元素进行比较。由于数据是有序的，系统可以排除一半的搜索空间。然后对剩余的一半递归地继续此过程，直到系统找到要搜索的值。

例如，给定有序数组 1,2,6,7,8,9,10。当搜索值 10 时，系统首先将其与中间值（7）进行比较，发现目标值大于 7，因此可以安全地跳过左半部分，因为它确信那些值将小于 7，所以 10 不可能存在于左半部分。

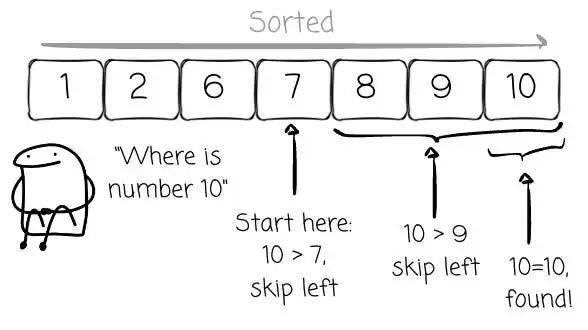
因此，该搜索过程的平均时间复杂度为 O(logn)。这里的关键是数组必须是有序的。

回到 BST，它通过以下约束提供了二分搜索性质：

每个节点最多有两个子节点

一个节点左子树中的所有节点都小于该节点

一个节点右子树中的所有节点都大于该节点

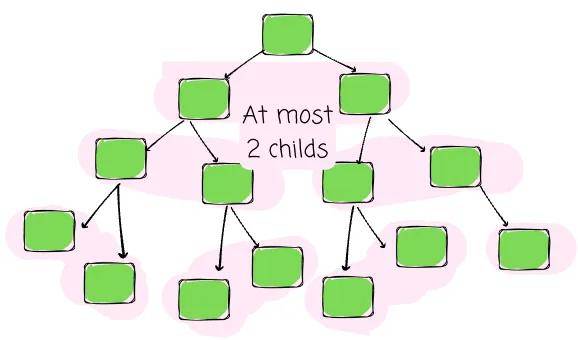
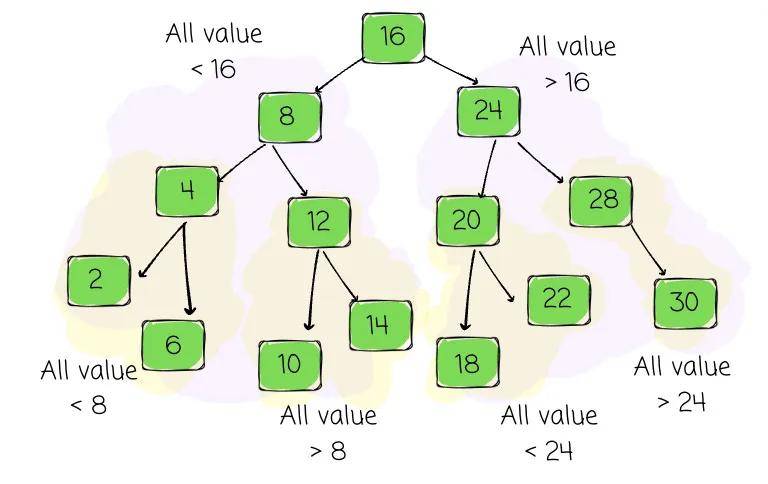
这种严格的排序使系统能够执行类似于上述有序数组上的搜索算法。

与有序数组从中间开始不同，这里从树的根开始，将搜索值与当前节点的值进行比较，如果目标较小，则递归地进入左子树，如果较大，则进入右子树。此过程持续，直到找到键（或最终发现值不在树中）。

我曾经想知道为什么我们不直接使用数组结构来实现二分搜索性质。答案很简单：数组可以为读操作提供该性质，但添加或删除数据的复杂度仍然是 O(n)。

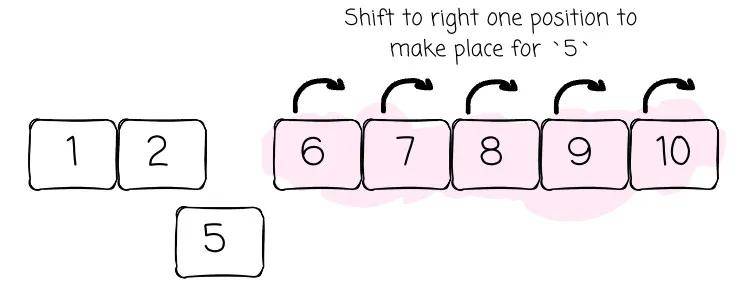
这是因为，当我们在数组的开头或中间添加或删除一项时，数组需要移动数据以确保其在内存中连续存储。

BST 为读和写操作都提供了二分搜索性质。代价是管理 BST 更加复杂，特别是在确保添加或删除数据仍然遵守 BST 约束方面。

三、平衡

然而，仅仅遵守约束并不能完全保证操作的 O(logn) 复杂度；另一个重要因素是树必须平衡。在一棵理想平衡的树中，每个节点的左右子树拥有大致相同数量的节点，这使得搜索、插入和删除操作的平均时间复杂度为 O(log n)，因为每次比较都能有效地将剩余搜索空间减半。

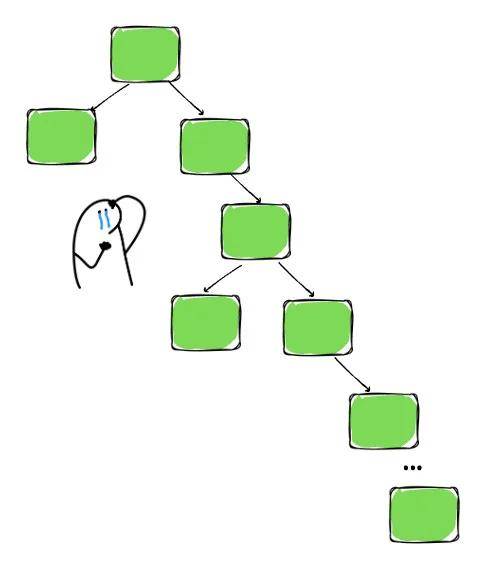
想象一下，一棵树的根节点值为 10。左子树只包含一个值（9），而右子树包含超过 20 个值（从 11 到 30）。因此，搜索一个大于 10 的值需要系统遍历树中几乎每一条记录。二分搜索的好处荡然无存。

有一些 BST 实现可以自平衡，例如AVL树或红黑树。由于篇幅所限，本文不会深入探讨这些实现的细节。

只需记住这一点，当我们继续探索 B-Tree 时，因为平衡是优化树性能的关键。

四、二叉树在磁盘上不能很好地工作

二叉搜索树在读写操作上都具备的二分搜索性质，对许多应用来说非常有吸引力，包括数据库，特别是像 PostgreSQL 这样的关系型数据库，其中大多数工作负载都涉及尽可能快地读写单条记录。

然而，BST 是为在内存中工作而设计的。给定内存对随机访问很快，跟随指针到节点位置是快速的。

在磁盘上进行随机访问则是另一回事。

从内存数据结构转向为硬盘驱动器（HDD）或固态驱动器（SSD）设计的数据结构，需要一次根本性的范式转变。

主要挑战是主存与磁盘之间的延迟差距。内存访问以纳秒计，而 HDD 上的一次寻道操作可能需要毫秒——相差四到五个数量级。即使现代 SSD 消除了机械寻道时间，延迟仍以微秒计，使得磁盘访问远比内存访问慢。

因此，这里的目标是最小化磁盘 I/O 操作次数。

此外，磁盘以块为单位工作。当读取或写入磁盘时，涉及的是固定大小的数据块（例如 4 KB、8 KB 或 16 KB）。因此，建立在磁盘上的高效数据结构必须对齐这种访问模式，旨在从其读取的每个页面中提取最大可能的价值。

现在你可以看到，为何在磁盘上使用 BST 是个问题。

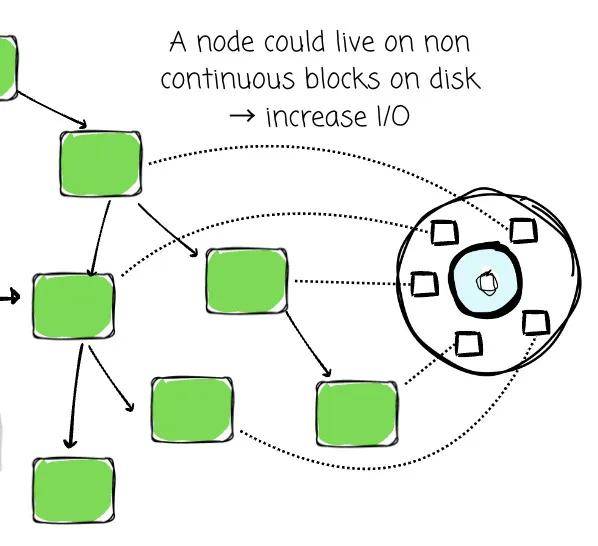
每个节点存储一个值和两个指向其子节点的指针，给定一棵高度为 20 的平衡 BST。为了找到一个条目，我们必须遍历树，一次跟随一个指针。这可能意味着多达 20 次独立的磁盘读取，因为每个节点可能位于磁盘上不同的、不连续的块中。

此外，由于一个节点只包含少量数据（数据和两个指针，总共几十个字节），用一个完整的磁盘块来表示一个节点会浪费存储和 I/O 带宽。

五、B树

鉴于大多数关系型数据库将数据存储在磁盘上，它们需要对 BST 进行改进。于是 B-Tree 出现了。

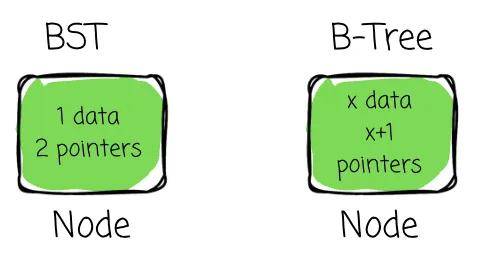
它于 1970 年代被提出，并自此无处不在。它是一种自平衡搜索树，通过允许每个节点包含许多键并拥有许多子节点，对 BST 进行了泛化。一个节点现在存储更多数据，这与基于磁盘块的布局对齐，确保每次 I/O 操作都尽可能富有成效。

B-Tree 将数据库拆分为固定大小的页面。一次读取或写入一个页面。页面大小（例如，PostgreSQL 页面大小为 8 KB）必须与磁盘块大小对齐，以确保磁盘访问性能。

注意：从此时起，我将交替使用 `page` 和 `node` 来指代 B-Tree 中的一个节点。

六、剖析

在经典的 B-Tree 实现中，数据可以存储在非叶子节点中。在变种 B+ Tree 中，只有叶子节点保存数据。

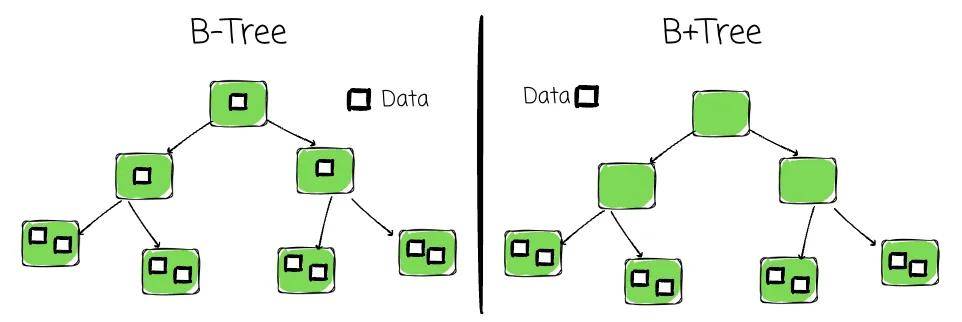
这使得所有数据操作都能专注于叶子节点。B+ Tree 已被广泛采用，通常人们所说的 B-Tree 就是指 B+ Tree。本文余下的部分描述的即是 B+ Tree 的实现，其中数据仅存储在叶子中。

在 B+Tree 中有一个至关重要的因子，叫做树的阶，称为 M，它表示一个页面可以指向的子节点的最大数量。每个节点最多有 N 个键，其中 N = M - 1。此外，一个节点必须至少有 N/2 个键，以确保节点至少半满，避免空间浪费，并保持高效的结构。

像一般树一样，B+ Tree 也有：

一个根节点：每个数据操作都必须从这里开始。

叶子节点存储指向实际数据的指针。更详细地说，它们存储键值对；键是索引列的值，值是指向实际数据的指针。
内部节点将根和叶子连接在一起。

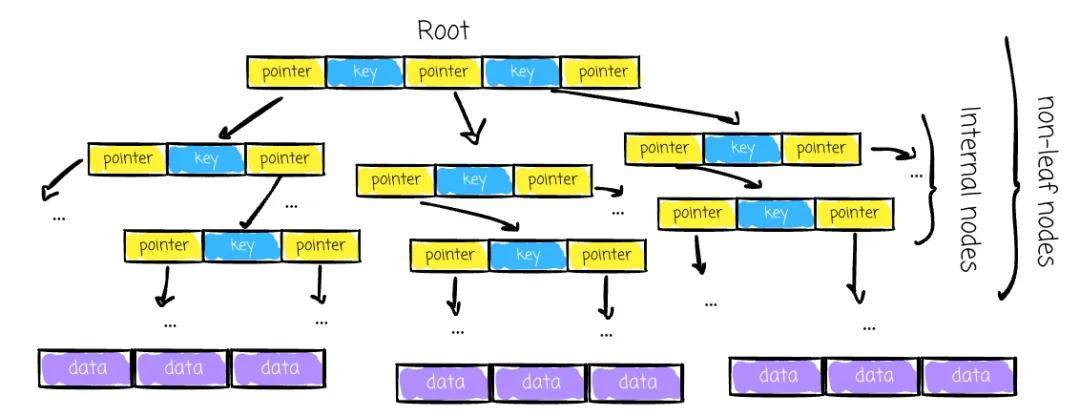
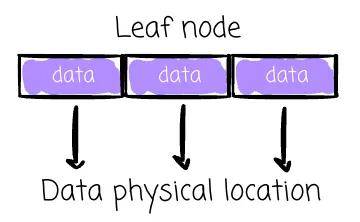
对于非叶子（根和内部）节点，它们存储：

键，即索引列的值。非叶子节点将拥有一段连续的排序键（排序以启用二分搜索）。
指向其他节点的指针。
指针的数量等于键的数量 + 1。
指针将指向一个子树，该子树的键范围在 [ key_left, key_right )

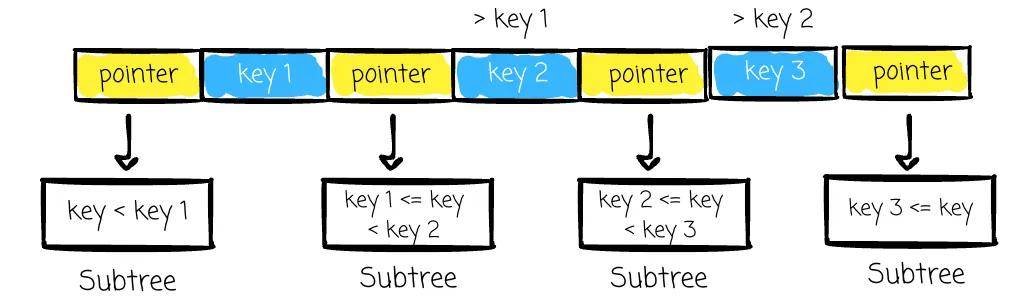
数据操作归结于找到所需的数据节点。读取和更新数据是类似的过程。更详细地说，过程如下：

一个带有索引列过滤器的查询，可以是点查找或范围过滤（=、<、>、between），例如通过客户 ID 获取客户。（此查询在 OLTP 工作负载中非常普遍）
搜索操作从树的根节点开始。
数据库将搜索值与节点中存储的键进行比较，以确定跟随哪个子指针。
此过程重复进行，一次下降一层，直到到达包含所需数据的叶子节点。

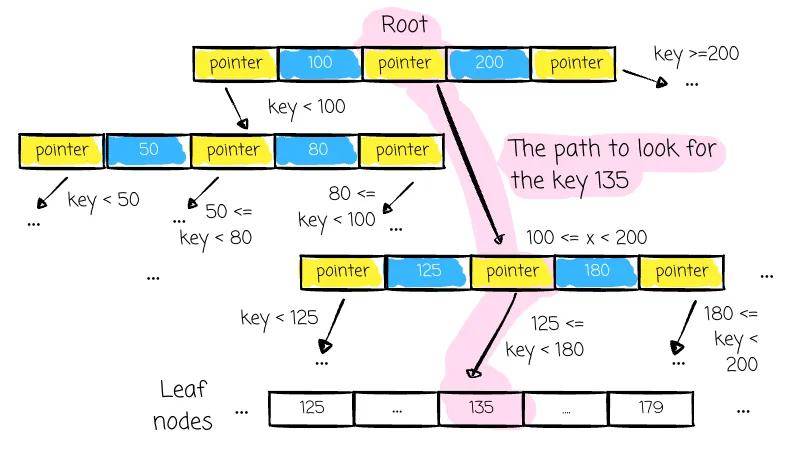
七、节点已满

如前所述，插入涉及通过访问根节点然后跟随后代指针来查找所需的叶子节点。如果节点有空闲空间，系统随后可以插入新键。然而，当一个节点已满时，挑战出现了；插入键会导致其超过最大键数 N。这种行为通常称为溢出。

为了解决此问题：

创建一个最大容量为 N 的新节点。
溢出节点中从位置 (N/2) + 1 开始的数据将被移动到新创建的节点中。

然后，系统在父节点中添加关联的键和指针。这种行为取决于溢出节点是叶子节点还是非叶子节点：

如果它是叶子节点，新节点的第一个键将被复制到父节点中。

如果它是非叶子节点，新节点的第一个键将被移动到父节点中。

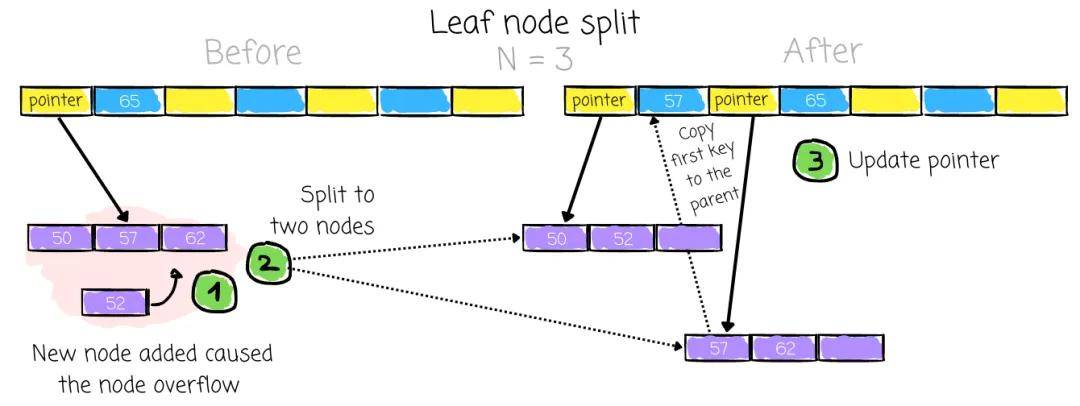
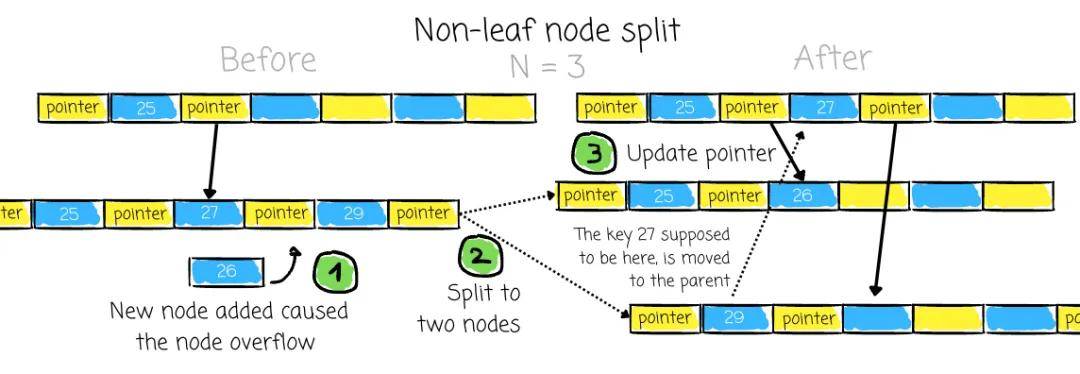
对于叶子节点的情况，通过将此键复制到父节点，该键现在充当导航指南。父节点说：“任何小于该键的去我的左孩子，任何大于或等于该键的去我的右孩子。”

对于内部节点的情况，将此键移动到父节点充当分割。它不再需要存在于子节点级别，因为它的唯一目的是分割那些现在位于两个独立节点中的键。由于此级别没有数据指针，移动该键不会导致丢失对任何数据的访问。

如果父节点也溢出了，它们也必须被分裂。这种分裂操作可能需要递归地一直进行到根节点。

八、节点未充分利用

与溢出相反的情况，称为下溢，即一个节点包含的键数少于最小键数限制（N/2）。这可能在用户删除数据时发生。解决此情况的过程与系统解决溢出的方式正好相反。

想法很简单：如果两个相邻节点（兄弟节点）拥有同一父节点，并且它们的总键数可以放入一个节点中，它们应该被合并：

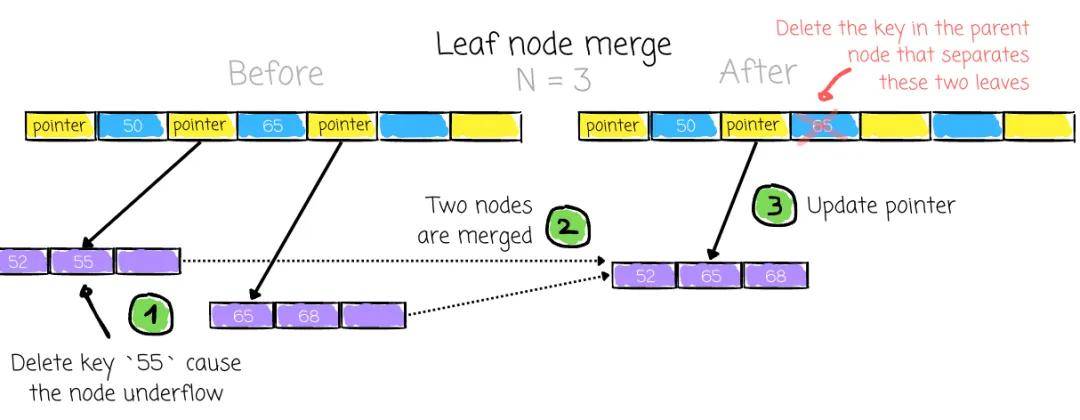
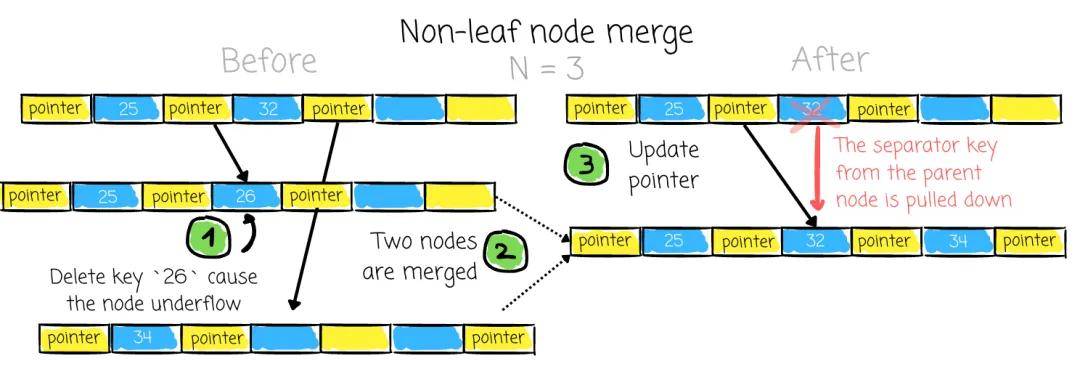
如果它是叶子节点，它与相邻兄弟节点合并。一个节点的所有键指针对被移动到另一个节点中。结果是一个包含两者所有键的单一叶子节点。分隔这两个叶子节点的父内部节点中的键被删除。

如果它是非叶子节点，它也与相邻兄弟节点合并。系统必须首先拉下其父节点中的分隔键。该键加入两个待合并节点的键中。下溢节点、其兄弟节点以及拉下的父键的所有键和所有子指针被合并成一个新的单一内部节点。

与溢出情况一样，解决下溢的过程可能需要一直进行到根节点。

九、使其可靠

本质上，B-Tree 中的写操作会用新数据覆盖磁盘页面。某些操作还涉及同时处理磁盘上的多个页面（例如，分裂一个页面）。两个分裂页面被写入，外加可能多个父节点也将被更新。如果由于在此过程中发生问题，只有其中一个页面被写入怎么办？

为了提供持久性，B-Tree 的实现普遍采用预写日志（WAL）。它是一个仅追加的文件。系统必须将任何 B-tree 修改写入此文件，然后才能将其应用于页面。当数据库在崩溃后恢复时，此日志用于将 B-tree 恢复到一个一致的状态。

结语

在本文中，我们重温了树数据结构的基础知识，重点介绍了具备二分搜索性质的二叉搜索树（BST）。接着我们探讨了这一性质对许多应用的吸引力，包括关系型数据库。然后，我们研究了为何 BST 不适合磁盘布局。文章的其余部分深入探讨了 B-Tree 的实现（更准确地说是 B+Tree），从它的解剖结构到如何重新分配节点（分裂与合并）。

尽管 B-Tree 在数据读取方面表现优异，但写操作需要更多工作来确保树的结构。未来，我们将看到一种更侧重于写方面的替代实现。令人兴奋的是，这种解决方案在 OLAP 世界中更为常见；它就是 LSM 树。

>>>>

参考资料